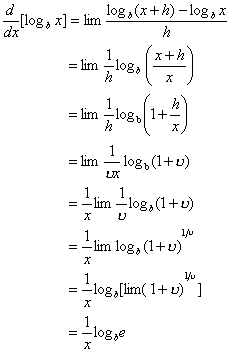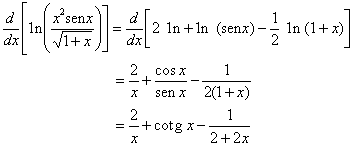PITÁGORAS

Pitágoras é considerado um dos grandes matemáticos da Antiguidade. Pitágoras nasceu por volta de 580 a.C. na ilha grega de Samos. Viajou bastante pelo mundo, tendo visitado o Egipto e Babilónia, onde entrou em contacto com matemáticos, tendo conhecimento dos seus estudos sobre os conjuntos de números, agora com o seu nome, os triplos pitagóricos, e que já eram conhecidos dos cientistas e matemáticos babilónicos há mais de 1500 anos.

Fresco de Raphael

Os aspectos matemáticos dos magníficos trabalhos de arte e arquitectura, tais como os Jardins Suspensos, em Babilónia, e a Esfinge e as Pirâmides no Egipto, bem como outras das sete maravilhas do mundo antigo não devem ter passado despercebidos a Pitágoras, que deve também ter sido confrontado com as ideias religiosas e filosóficas do Oriente.

Quando voltou à Grécia, Pitágoras abandonou a ilha de Samos e mudou-se para Crotona, na "bota" italiana, que, assim como a maior parte do Sul da Itália fazia parte do mundo grego e aí fundou a Escola Pitagórica, cujo lema era "O número é tudo".

É-lhe atribuída a descoberta do Teorema de Pitágoras, que tem uma forte influência nos triplos pitagóricos.(Se deseja ver o Teorema de Pitágoras com animação no GSP consulte a página Escola Pitagórica).O teorema em si teve origem na Babilónia, séculos antes, visto que os Babilónios compreendiam muito bem os triplos "pitagóricos". No entanto, os pitagóricos relacionaram-no com a geometria, generalizando o problema para além dos números naturais.

Os pitagóricos acreditavam firmemente que a essência de tudo, quer na geometria, quer nas questões praticas e teóricas da vida do homem, podia ser explicada através das propriedades dos números inteiros e/ou das suas razões.

A Pitágoras deve-se também o conceito geométrico do espaço, como ente contínuo e ilimitado, o estudo e construção dos poliedros regulares e o dos polígonos.

Pelo estudo das propriedades das figuras, traduzindo-se por meio de relações entre números, e das propriedades dos números em relação com a geometria, chegou à noção de número irracional e de grandezas incomensuráveis.

É muito difícil senão impossível, separar, nas investigações pitagóricas, a parte de Pitágoras da dos seus discípulos pois que, além do isolamento, era princípio da Escola Pitagórica que todos os conhecimentos deviam ser considerados como adquiridos em comum.

Depois da morte de Pitágoras por volta de 500 a. C. e da destruição do centro de Crotona, onde a maioria dos membros da Escola Pitagórica foram mortos, a filosofia e o misticismo dos números espalhou-se pelo mundo grego através dos restantes pitagóricos.

Filolau de Tarento aprendeu a filosofia da matemática através desses refugiados e foi o primeiro filósofo grego que escreveu a história e as teorias dos pitagóricos. Platão aprendeu a filosofia pitagórica dos números, a cosmologia e o misticismo através deste livro escrito por Filolau.

Posteriormente, o pitagórico Teodoro de Cirene (450 A. C.), como Platão indica no Teeteto, provava geometricamente que os números Ö 3, Ö 5, ...Ö 17, são incomensuráveis com a unidade. Nos Diálogos, Platão apresenta Teodoro, seu mestre, no acto de ensinar esta propriedade aos próprios discípulos mediante desenhos geométricos.

Decomposição em factores

1. Determine as multiplicidades algébricas das raízes do polinómio

   A(x) = 2x² + 2x - 4 = 0.

   Resolução: As raízes reais de A são

   

   Podemos então escrever

   A(x) = 2(x – 1)(x + 2).

   e assim, porque o polinómio Q(x) = 2 não tem obviamente raízes reais, vemos por (4) que 1 e -2 são raízes simples de A.

2. Classifique as raízes do polinómio

   A(x) = 4x² - 4x + 1.

   Resolução: O polinómio A tem uma única raiz real dada por

   

   Podemos então escrever

   

   e assim, porque o polinómio Q(x) = 4 não tem raízes reais, vemos por (4) que é uma raiz dupla de A.

Um pouco da História dos Logaritmos

Os logaritmos, como instrumento de cálculo, surgiram para realizar simplificações, uma vez que transformam multiplicações e divisões nas operações mais simples de soma e subtração.

Napier foi um dos que impulsionaram fortemente seu desenvolvimento, perto do início do século XVII. Ele é considerado o inventor dos logaritmos, muito embora outros matemáticos da época também tenham trabalhado com ele.

Já antes dos logaritmos, a simplificação das operações era realizada através das conhecidas relações trigonométricas, que relacionam produtos com somas ou subtrações. Esse processo de simplificação das operações envolvidas passou a ser conhecido como prostaférese, sendo largamente utilizado numa época em que as questões relativas à navegação e à astronomia estavam no centro das atenções. De fato, efetuar multiplicações ou divisões entre números muito grandes era um processo bastante dispendioso em termos de tempo. A simplificação, provocada pela prostaférese, era relativa e, sendo assim, o problema ainda permanecia.

O método de Napier baseou-se no fato de que associando aos termos de uma progressão geométrica

b, b², b³, b⁴, b⁵, … , bⁿ, …

os termos da progressão aritmética

1, 2, 3, 4, 5, ... , n, ...

então ao produto de dois termos da primeira progressão, b^m.b^p, está associada a soma m+p dos termos correspondentes na segunda progressão.

Considerando, por exemplo,

PA	1	2	3	4	5	6	7	8	9	10	11	12	13	14
PG	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16394

Para efetuar, por exemplo, 256 x 32, basta observar que:

• 256 na segunda linha corresponde a 8 na primeira;
• 32 na segunda linha corresponde a 5 na primeira;
  
• como 8+5=13,
  
• 13 na primeira linha corresponde a 8192 na segunda.

Assim, 256x32=8192 resultado esse que foi encontrado através de uma simples operação de adição.

A fim de que os números da progressão geométrica estivessem bem próximos, para ser possível usar interpolação e preencher as lacunas entre os termos na correspondência estabelecida, evitando erros muito grosseiros, Napier escolheu para razão o número = 0,9999999, que é bem próximo de 1. Segundo Eves, para evitar decimais, ele multiplicava cada potência

Howard Eves é o autor do livro Introdução à História da Matemática. A referência é a da tradução de Hygino H. Domingues, 2^a edição, Editora da UNICAMP, Campinas, SP, 1997

por . Então, se , ele chamava L de "logaritmo" do número N.

Assim, o logaritmo de Napier de é 0 e o de é 1.

Enquanto Napier trabalhava com uma progressão geométrica onde o primeiro termo era 10⁷.b e a razão b, ao que parece, de forma independente, Bürgi também lidava com o problema dos logaritmos.

Bürgi empregou uma razão um pouco maior do que 1, qual seja 1,0001=1+10^-4. O primeiro termo de sua PG era 10⁸ e ele desenvolveu uma tabela com 23027 termos.

Como Napier, Bürgi considerou uma PG cuja razão era muito próxima de 1, a fim de que os termos da seqüência fossem muito próximos e os cálculos pudessem ser realizados com boas aproximações.

Posteriormente, Napier, juntamente com Briggs, elaboraram tábuas de logaritmos mais úteis de modo que o logaritmo de 1 fosse 0 e o logaritmo de 10 fosse uma potência conveniente de 10, nascendo assim os logaritmos briggsianos ou comuns, ou seja, os logaritmos dos dias de hoje.

Ainda segundo Eves, durante anos ensinou-se a calcular com logaritmos na escola média ou no início dos cursos superiores de matemática; também por muitos anos a régua de cálculo logarítmica foi o símbolo do estudante de engenharia do campus universitário.

Hoje, porém, com o advento das espantosas e cada vez mais baratas e rápidas calculadoras, ninguém mais em sã consciência usa uma tábua de logaritmos ou uma régua de cálculo para fins computacionais. O ensino dos logaritmos, como um instrumento de cálculo, está desaparecendo das escolas, os famosos construtores de réguas de cálculo de precisão estão desativando sua produção e célebres manuais de tábuas matemáticas estudam a possibilidade de abandonar as tábuas de logaritmos. Os produtos da grande invenção de Napier tornaram-se peças de museu.

A função logarítmica, porém, nunca morrerá pela simples razão de que as variações exponencial e logarítmica são partes vitais da natureza e da análise. Conseqüentemente, um estudo das propriedades da função logarítmica e de sua inversa, a função exponencial, permanecerá sempre uma parte importante do ensino da matemática.

Recentemente, no século XX, com o desenvolvimento da Teoria da Informação, Shannon descobriu que a velocidade máxima C_máx - em bits por segundo - com que sinais de potência S watts podem passar por um canal de comunicação, que permite a passagem, sem distorção, dos sinais de freqüência até B hertz, produzindo um ruído de potência máxima N watts, é dada por:

FUNÇÃO LOGARÍTMICA

John NEPER (1550 - 1617)

A invenção dos logaritmos ( palavra de origem grega:(logos) = tratado, arithmos (ariqmos) = números), deve-se ao matemático escocês John Napier, barão de Merchiston (1550-1617), que se interessou fundamentalmente pelo cálculo numérico e pela trigonometría. Em 1614, e ao fim de 20 anos de trabalho, publicou a obra Logarithmorum canonis descriptio, onde explica como se utilizam os logaritmos, mas não relata o processo como chegou a eles Um ano depois, em 1615, o matemático inglês Henry Briggs (1561-1631), visitou Napier e sugeriu-lhe a utilização da base 10. A Napier agradou-lhe a ideia e resolveram elaborar as respectivas tábuas dos logaritmos decimais. Com a morte de Napier é Brigs que conclui o trabalho e em 1618, publica Logarithmorum Chiliaes prima, primeiro tratado sobre os logaritmos de base 10 e faz o calculo para os números de 1 a 20 000 e de 90 000 a 100 000

Já conhecemos as operações :adição, subtração,multiplicação, divisão, potenciação e radiciação. Vamos agora introduzir duas novas operações: a logaritmização e a exponenciação.

Os logaritmos vêm facilitar a vida na medida que vão permitir simplificar cálculos mais complicados. E porque ? por que com eles vamos baixar o grau de dificuldade das operações transformando:

multiplicações em adições
divisões em subtracções
potenciação em multiplicação
radiciação em divisão

• Definição de logarítmo :

Chama-se logaritmo de x na base a a um número b tal que se elevarmos a ao expoente b obtemos x:

Exemplo:

generalizando:

b será portanto o logarítmo de x na base a o que significa que b é o expoente a que deve ser elevado a para obter x.

Exemplos:

1- log₁₀ 1000=3 pois 10³ =1000

2- log₃ 81 = 4 já que 3⁴ = 81

Uma nota:

Vamos tentar calcular manualmente o log₂10 . Como 2³<10<2⁴ o valor do log será um número entre 23 e quatro logo do tipo 3,... Assim já temos a chamada característica do logaritmo (isto é a parte inteira) podemos procurar uma primeira casa décimal , de facto 2^3.4=10.55 e 2^3.3=9.84 concluimos que a parte decimal inicia-se com 3 e log₂10=3,3.... mantissa ( do latim excesso).

Então o logaritmo de um número será da formma c,m onde c Z e 0<m<1

A base a é sempre um número real e positivo diferente de 1 . Qual a razão ?

Calculadora de logaritmos Um scrip simples para calcular logaritmos Base do logaritmo: Número: Resultado:

• Propriedades e regras operatórias:

Do exposto verifica-se que a función logarítmica é uma aplicação bijectiva do conjunto R⁺ , sobre o conjunto dos reais :

Veremos mais tarde que a inversa da função logarítmica é a denominada função exponencial.

• Estudo da Função Logarítmica :

Chama-se função logaritmica à função real de variável real :

A função logaritmica é uma aplicação bijectiva de R⁺ em R :

Observações:

• Os números negativos e o zero não têm logaritmo
• A função logaritmica de base a é a reciproca da exponencial de base a ou seja: y = a^x
• As funções logaritimicas mais usuais são as de base 10 (log. decimais) e as de base e =2,718281 (log. naturais).

---

• Gráfico da função logarítmica :

a>1
0<a<1

• Logaritmos decimais :

A base mais utilizada é a base 10 ou seja os logaritmos decimais é por essa razão que muitas vezes, neste caso, se omite a base

Vejamos um exemplo de como os logaritmos podem facilitar os cálculos usando as regras anteriormente dadas no quadro :

• Logaritmos Neperianos ou de base natural :

Estes logaritmos que tem por base o número e (base de Neeper) e escreve-se muitas vezes .

• Mudança de base :

Exemplo : Determina log3 7 com aprox. de 6 decimais. De antemão sabemos que a resposta será um número entre 1 e 2 pois 31 = 3 e 32 = 9 , e o 7 está entre 3 e 9. Vamos mudar a base dos logaritmos para 10, log3 7 pode se escrever como . ou mais simplesmente . Utilizando a calculadora teremos:: Claro está que se fossemos verificar a validade do resultado fariamos. Que é um resultado aproximado como desejavamos

• Antilogaritmo :

É o número que corresponde a umlogaritmo dado. Consiste no problema inverso do cálculo do logaritmo de um número.

ou o que é omesmo: consiste em elevar a base ao número obtido no logaritmo :

ver exponencial

• Cologaritmo :

Designa-se por cologaritmo de um número x ao logaritmo do seu recíproco ou inverso :

justifica a segunda parte desta igualdade

• Alguns valores uteis

• Equações logarítmicas :

Trata-dse de equações que à incógnita foi aplicada a operação logaritmo.

É fácil concluir que a igualdade entre os logaritmos de duas expressões implica a igualdada de ambas. (este é o principio em que se fundamenta a resolução deste tipo de equações ou o que se poderá dizer de outra maneira: aplicando o antilogaritmo)

Exemplo:

log x = log (x³+5) + 10x = x³ +5 + log 10 x = x³+5 +1

• Sistemas de Equações logarítmicas :

Como é fácil depreender trata-se de um sistema de equações em qua (as) incógnita(s) estão sugeitas à operação logaritmo. A sua resolução faz-se como normalmente outros sistemas só que tendo em atenção as propriedades dos logaritmos para efectuar as transformações necessárias.Exemplo :

• A recordar...

Se a > 1
Os números menores que 1 têm logaritmo negativo
Os números maiores que 1 têm logaritmo positivo

Se 0 < a < 1
Os números menores que 1 têm logaritmo positivo
Os números maiores que 1 têm logaritmo negativo

Respostas

1- 7 basta atender à def. de logaritmo

2- 10² x 10^{log 3}= 100 x 3

3- log₈ 8²+ log₄4³= 2 + 3

4- log₅ (375 / 3)= log₅ 125 = 3

5= log 32/log 16 (pela mudança de base) logo: log 2⁵/log 2³= 5/4

6-3x+1= 4² aplicando log₄ a ambos os membros

7- x³ = 343 logo x=...

8- x²=6-5x logo x=... (atenção às sol. apresentadas!)

9- log (2 x 3)= log2 + log3= a+b

10-log 7²= 2 log 7=...

11-log 2^0.5 =...

12-log(7 x 100) = log 7 +log100=...

13- log 2^-3 =...

14- log 2/log 3=...

15-

16- log(x - 5)

log(x + 4) = log 10 - log(x - 5) = log (10/(x - 5))

x + 4 = 10/(x - 5)

x² - x - 30 = 0

x = 6
x = - 5 (esta solução não é válida).

Problemas de Logaritmos

Calcula: 1) 10 log 7 2) 102+log 3 3) log 8 64+ log4 64 4) log 5 375 - log 5 3 5)log 16 32

Resolve : 6) log 4 (3x+1)=2 7) log x 343 =3 8) log x(6-5x))=2

Sabendo que log 2 =a; log 3 =b; log 7 =c determina:

9) log 6 10) log 49 11) log2

12) log 700 13) log 0.125 14) log3 2

Resolve as equações:

15)	16) log(x + 4) = 1 - log(x - 5)

Funções Logarítmica e Exponencial

DERIVADAS DE FUNÇÕES LOGARÍTMICAS E EXPONENCIAIS

Agora obteremos fórmulas das derivadas para as funções logarítmicas e exponenciais e discutiremos as relações gerais entre e derivada de uma função um a um e a sua inversa.

• DERIVADAS DE FUNÇÕES LOGARÍTMICAS

O logaritmo natural desempenha um papel especial no cálculo que pode ser motivado diferenciando , onde b é uma base arbitrária. Para esta proposta, admitiremos que é diferenciável, e portanto contínua para x > 0. Também necessitaremos do limite

Usando a definição de derivada, obtemos(com x em vez de v como variável).

Assim,

Mas a partir da fórmula , temos = 1/1n b; logo, podemos reescrever esta fórmula de derivada como

No caso especial onde b = e, temos = 1n e = 1, logo esta fórmula torna-se

Assim, entre todas as possíveis bases, a base b = e produz a fórmula mais simples da derivada para . Esta é uma das razões por que a função do logaritmo natural é preferida sobre todos os logaritmos no cálculo.

Exemplo 1

Ache

Solução. A partir de

Quando possível as propriedades dos logaritmos devem ser usadas para converter produtos, quocientes e expoentes em somas, em diferenças e em múltiplos de constantes, antes de diferenciar uma função envolvendo logaritmos.

Exemplo 2